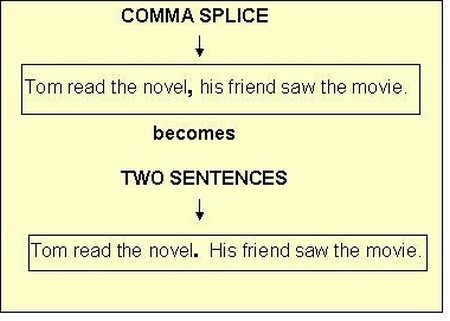
Many students find difficult to end the sentence with full stop for you people it may be surprising question but it is fact. And it is not easy to define a sentence as it is not that simple. Everyone can’t define it in well manner on their own. In many dictionaries they tried to define a sentence that what is sentence basically. But there is some disagreement about this. For simple and common understanding, we may define it like, “A sentence is a group of words that makes complete sense of understanding.” For instance, Sam is a bright boy. Judy runs on the beach everyday.
Simple Sentence
The most basic unit of construction of sentence is making the singular idea with the help of words in the form of group placed together especially when in writing the paragraph. There are many types of sentences they come in different verities of structures and lengths. And with the combination of different words a complex and long sentence forms. However, sentences can also be simply constructed and very brief. These sentences are known as simple sentences. A simple sentence is basically named that implies that a sentence of simple construction. It contains only one subject and one predicate. And this is lacking of any subordinate or dependent clauses in sentence. A simple sentence is the most basic type of sentence written and is often brief and to the point.
Compound Sentence
A compound sentence is the sentence which contains two independent parts and they are linked together. It is must to have linked word between two parts or clauses by some kind of conjunction to make the compound sentence. The compound sentence may take some kind of conjunction like correlative conjunction, a coordinating conjunction or even a semicolon functioning as a conjunction. In compound sentences a ‘comma’ is often used to help compensate the two independent clauses as well, although it is not usually needed grammatically.
Complex Sentence
Basically the complex sentence is made by minimum two clauses the one is dependent clause and the other one is independent clause. It is one in English but made with the help of two parts. The first one is dependent clause and it is also called the subordinate clause and it is connected by either a relative pronoun or subordinate conjunction. And the complex sentence may also be contrasted with a simple sentence, which has no dependent clause. And the other type of sentences includes the compound sentence. And the compound sentence need to have at least two independent clauses, and are the complex-compound sentences and they need to have at least two independent clauses, and at least one dependent clause.
Compound-Complex Sentences
A compound-Complex sentence is made up of two or more than two independent parts and on or more than one subordinate clause.
Just like the name implies, generally it is made up of a complex sentence and compound sentence. For instance, Rachael Ray explained how cookies are made, and we practiced her techniques at home.